Here’s a cool problem I came across when reviewing for one of my calculus exams:

You begin with the numbers 0 through 1. Every iteration removes 1/3 from the remaining segments. As stated above, the expression for the total amount removed after m iterations is:
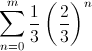
The first iteration removes 1/3. The second removes 1/3 from the remaining two segments. The remaining segments are 1/3 long, and 1/3 of that is 1/9. We do that once for each remaining segment, so 2/9 is removed. And so on.

What if we iterate an infinite number of times? Then we have a convergent geometric series. Finding the sum is easy:

So, what’s the total amount or length of numbers removed? 1. That’s the entire length. It seems like we’ve removed the entire segment. But wait a minute. If we look at the image of the original question above, we see that after every iteration, there are 2n+1 segments remaining. When n=0, there are 2 segments. When n=1, there are 4 segments, etc. As we remove more and more, 2n+1 approaches infinity. In other words, the limit does not exist, and the number of segments goes to infinity.

So, even though we’ve seemingly removed the entire length, there are an infinite number of segments remaining.